题目描述

You are given an undirected unweighted graph with $N$ vertices and $M$ edges that contains neither self-loops nor double edges.
Here, a self-loop is an edge where $a_i = b_i (1≤i≤M)$, and double edges are two edges where $(a_i,b_i)=(a_j,b_j)$ or $(a_i,b_i)=(b_j,a_j) (1≤i \lt j≤M)$.
How many different paths start from vertex $1$ and visit all the vertices exactly once?
Here, the endpoints of a path are considered visited.

For example, let us assume that the following undirected graph shown in Figure 1 is given.

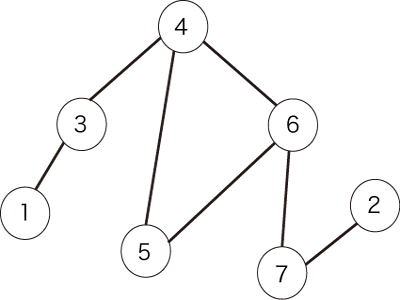
Figure 1: an example of an undirected graph

The following path shown in Figure 2 satisfies the condition.

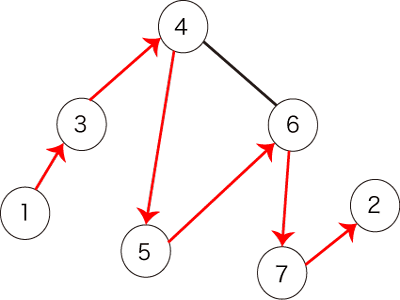
Figure 2: an example of a path that satisfies the condition

However, the following path shown in Figure 3 does not satisfy the condition, because it does not visit all the vertices.

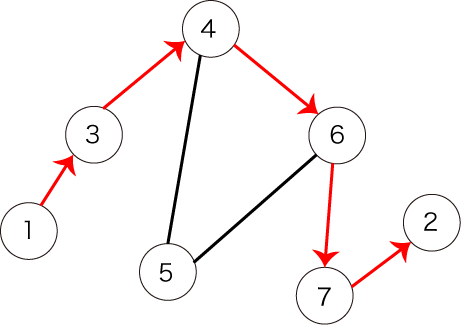
Figure 3: an example of a path that does not satisfy the condition

Neither the following path shown in Figure 4, because it does not start from vertex $1$.

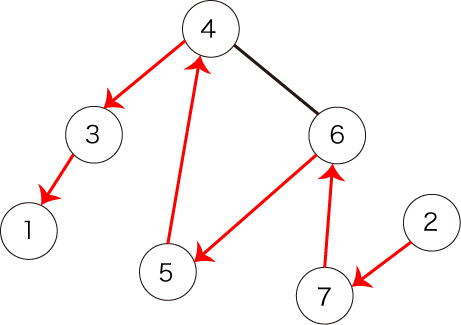
Figure 4: another example of a path that does not satisfy the condition

给你一个无向无权重图，该图有 $N$ 个顶点和 $M$ 条边，其中既没有自循环也没有双重边。
这里， $a_i = b_i (1≤i≤M)$ 处的一条边为_自循环边， $(a_i,b_i)=(a_j,b_j)$ 或 $(a_i,b_i)=(b_j,a_j) (1≤i \lt j≤M)$ 处的两条边为_双循环边。
有多少条不同的路径从顶点 $1$ 出发并恰好访问所有顶点一次？
在这里，路径的端点被视为已访问过的顶点。

例如，假设图 1 所示的无向图如下。

图 1：无向图示例

图 2 所示路径满足条件。

图 2：满足条件的路径示例

然而，图 3 所示的以下路径并不满足条件，因为它没有访问所有顶点。

图 3：不满足条件的路径示例

图 4 所示的路径也不满足条件，因为它不是从顶点 $1$ 开始的。

图 4：另一个不满足条件的路径示例

输入格式

输入内容按以下格式标准输入：

$N$ $M$
$a_1$ $b_1$
$a_2$ $b_2$
$:$
$a_M$ $b_M$

输出格式

打印从顶点 $1$ 出发并恰好访问所有顶点一次的不同路径的数量。

样例 #1

样例输入 #1

3 3
1 2
1 3
2 3

样例输出 #1

2

样例 #2

样例输入 #2

7 7
1 3
2 7
3 4
4 5
4 6
5 6
6 7

样例输出 #2

1

说明

数据规模与约定

• $2≦N≦8$
• $0≦M≦N(N-1)/2$
• $1≦a_i \lt b_i≦N$
• 给定图形既不包含自循环，也不包含双边。

样例 $1$ 解释

下图所示为给定图形：

下列两条路径满足条件：

样例 $2$ 解释

该测试用例与问题陈述中描述的测试用例相同。