题目背景

译自 Izborne Pripreme 2018 (Croatian IOI/CEOI Team Selection) D1T1。$\texttt{1s,1G}$。

题目描述

给定笛卡尔坐标系中的直方图，宽度为 $n$，第 $i$ 格的高度为 $h_i$。也就是说，对于 $\forall 1\le i\le n$，第 $i$ 格所占矩形的顶点坐标分别为 $(i-1,0),(i,0),(i-1,h_i),(i,h_i)$。

给定正整数 $p$，求出满足以下条件的矩形的数量：

• 矩形的四个顶点的坐标均为整数；
• 矩形有一条边在 $x$ 轴上；
• 矩形完全位于直方图内部（可以与边界相切）；
• 矩形的面积至少为 $p$。

输入格式

第一行，两个正整数 $n,p$。

第二行，$n$ 个正整数 $h_1,h_2,\ldots,h_n$。

输出格式

输出一行一个整数，表示答案。

6 9
1 4 4 5 2 3

3

10 5
3 6 1 3 2 1 5 3 4 2

31

提示

样例解释

样例一解释：

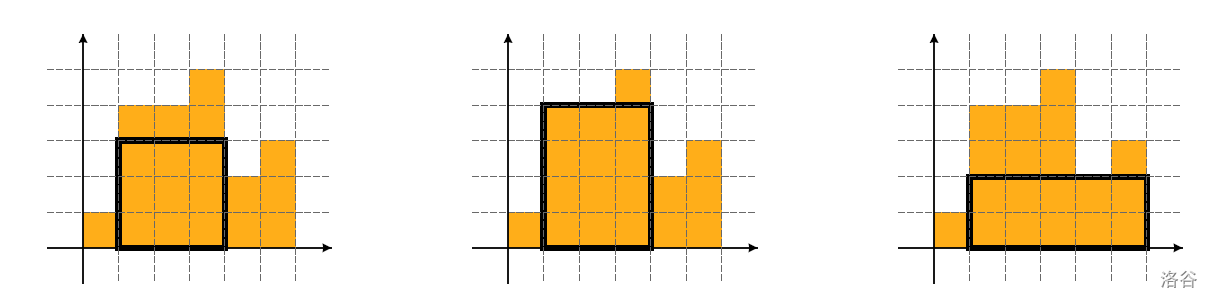
数据范围

对于 $100\%$ 的数据，保证：

• $1\le n\le 10^5$；
• $1\le p\le 10^{14}$；
• $1\le h_i\le 10^{9}$。