题目背景
翻译自 ROIR 2025 D1T3。
题目描述
有 n 个模块被运送到金星上用于组装实验室。模块按顺序排列,第 i 个模块的高度为 hi。
组装工作将由一台特殊的机器人来完成。在组装过程中,连续的模块段将逐渐合并,而模块在排列中的顺序不会改变。最初,每个模块都是一个独立的段,段的编号从 1 到 n,与模块的编号顺序相同。如果有两个相邻的模块段 A=[i,i+1,…,i+p−1] 和 B=[i+p,i+p+1,…,i+p+q−1],那么它们合并后变成段 $AB = [i, i+1, \dots, i+p-1, i+p, i+p+1, \dots, i+p+q-1]$。
组装指令由 n−1 条指令组成。每条指令包含一个数字 kj。执行该指令后,编号为 kj 和 kj+1 的模块段合并为一个新段,合并后的段占据原来两个段的位置,并重新对段进行编号,从 kj+2 开始,后面的段的编号依次减 1。执行完所有指令后,所有段将合并为一个段。
金星上常年下酸雨,因此在组装过程中,必须在每次合并后了解每个段中可能积累的液体量。设一个段包含高度为 hl,hl+1,…,hr 的模块。对于其中任意一个模块 p,其中 l≤p≤r,我们定义该模块 p 在该段的深度 dp 如下:
首先计算左侧最大高度 lp=max{hl,hl+1,…,hp} 和右侧最大高度 rp=max{hp,hp+1,…,hr}。这分别是该段中模块 p 左侧和右侧的最大高度。该模块 p 的深度定义为 dp=min(lp,rp)−hp,显然 dp>0。段的容量定义为该段所有模块的深度之和,即 w=dl+dl+1+⋯+dr。
给定一系列合并操作,请在每次合并后输出合并段的容量。
输入格式
第一行包含一个整数 n,表示模块的数量(2≤n≤105)。
第二行包含 n 个整数 h1,h2,…,hn(1≤hi≤109),表示每个模块的高度。
第三行包含 n−1 个整数,表示合并操作的指令,每个指令用一个整数 kj 表示(1≤kj≤n−j)。
输出格式
输出 n−1 个整数,用换行隔开,表示每次合并后,合并段的容量。
8
9 1 8 1 5 2 3 6
3 3 1 3 3 2 1
0
4
0
0
0
13
20
提示
下图显示了样例中指令执行的过程,每个模块上方标出了其深度,并显示了新段的容量。
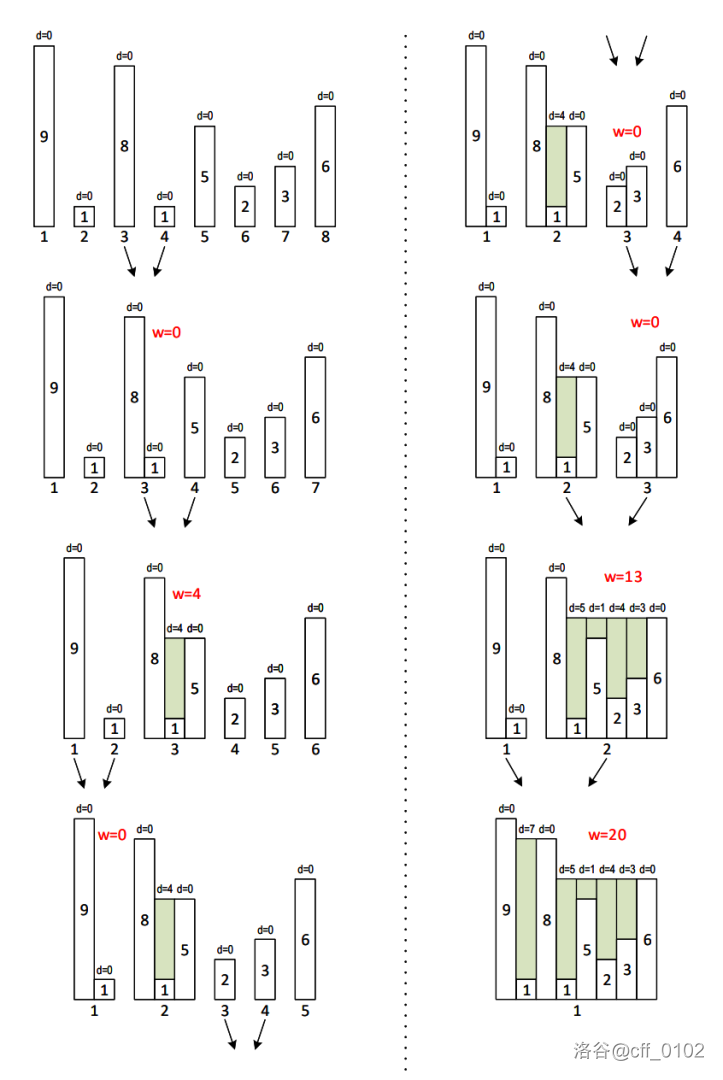
本题使用 Subtask 捆绑测试。数据中 Subtask 0 是样例。
| 子任务 |
分数 |
特殊性质 |
| 1 |
13 |
n≤100 |
| 2 |
n≤1000 |
| 3 |
hi≤10 |
| 4 |
$\exist i,h_1 \ge h_2 \ge \dots \ge h_i \leq \dots \leq h_n$ |
| 5 |
7 |
所有查询中 kj=1 |
| 6 |
13 |
n≤40000 |
| 7 |
28 |
无 |

