题目描述

在數學上，一個點集合 $S$ 的凸包 (convex hull) 定義為包含 $S$ 的最小凸集合，記作 $\operatorname{Conv}(S)$。在平面上，若 $S$ 為非空有限點集合，則 $\operatorname{Conv}(S)$ 為一包含內部與邊界的最小凸多邊形，或其退化形式。另一方面，設 $E_1$ 與 $E_2$ 為平面上的兩個點集合。若存在某個二維向量 $\mathbf{v}$，滿足

則稱 $E_1$ 與 $E_2$ 經過平移後重合。

現給定平面上的有限點集合 $S_1$ 與 $S_2$，並考慮它們的非空子集合 $T_1\subseteq S_1$ 與 $T_2\subseteq S_2$。已知子凸包 $\operatorname{Conv}(T_1)$ 與子凸包 $\operatorname{Conv}(T_2)$ 面積皆大於 $0$ 且經過平移後重合，請求出 $\operatorname{Conv}(T_1)$ 所有可能的面積。

以下展示兩個子凸包平移後重合的例子。

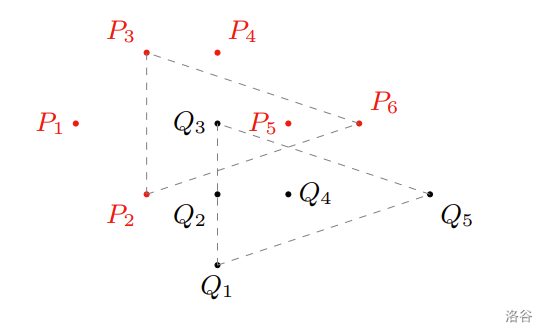
输入格式

$n$ $m$
$x_1$ $y_1$
$x_2$ $y_2$
$\vdots$
$x_n$ $y_n$
$\xi_1$ $\eta_1$
$\xi_2$ $\eta_2$
$\vdots$
$\xi_m$ $\eta_m$

• $n$ 代表 $S_1$ 的集合大小。
• $m$ 代表 $S_2$ 的集合大小。
• $x_i, y_i$ 代表 $S_1$ 包含點 $(x_i, y_i)$。
• $\xi_i, \eta_i$ 代表 $S_2$ 包含點 $(\xi_i, \eta_i)$。

输出格式

$k$
$a_1$
$a_2$
$\vdots$
$a_k$

• $k$ 代表若子凸包 $\operatorname{Conv}(T_1)$ 與子凸包 $\operatorname{Conv}(T_2)$ 經過平移後重合，$\operatorname{Conv}(T_1)$ 所有可能的非 $0$ 面積數。
• $a_i$ 為一整數，代表 $\operatorname{Conv}(T_1)$ 所有可能的非 $0$ 面積中，第 $i$ 小的數的兩倍。

提示

測資限制

• $3 \le n \le 40$。
• $3 \le m \le 40$。
• $0 \le x_i \le 20$。
• $0 \le y_i \le 20$。
• $0 \le \xi_i \le 20$。
• $0 \le \eta_i \le 20$。
• 對任意 $i, j \in \{1, 2, \ldots, n\}$，若 $i \ne j$，則 $(x_i, y_i) \ne (x_j, y_j)$。
• 對任意 $i, j \in \{1, 2, \ldots, m\}$，若 $i \ne j$，則 $(\xi_i, \eta_i) \ne (\xi_j, \eta_j)$。
• 輸入的數皆為整數。

評分說明

本題共有四組子任務，條件限制如下所示。 每一組可有一或多筆測試資料，該組所有測試資料皆需答對才會獲得該組分數。