题目背景

版权信息：译自 2025年度 国际情报 올림피아드 (Olympiad) 代表学生 选拔考试 R2T3。[CC BY-NC-SA 4.0]

题目描述

给定 $n$ 个点 $m$ 条边的无向连通图 $G=(V,E)$。图可能有重边，但没有自环。

点编号 $0\sim n-1$，边编号 $0\sim m-1$。

我们称整数数列 $a_0,a_1,\ldots,a_{n-1}$ 是完美的，当且仅当：

• 对于任意一条不重复经过一条边（可以重复经过点）的路径，设其依次经过的点编号为 $u_0,u_1,\ldots,u_{l-1}$，则以下条件必须满足：
  • 要么 $a_{u_0}\le a_{u_1}\le \cdots\le a_{u_{l-1}}$，要么 $a_{u_0}\ge a_{u_1}\ge \cdots\ge a_{u_{l-1}}$。

定义整数数列 $a_0,a_1,\ldots,a_{n-1}$ 的不等对数量为满足 $a_u\neq a_v$ 且 $0\le u\lt v\lt n$ 的二元组 $(u,v)$ 的数量。

求出完美数列不等对数量的最大值。

实现细节

你不需要，也不应该实现 main 函数。

你应当实现以下的函数：

long long max_diversity(int n, int m, std::vector<int> U, std::vector<int> V);  

• $n,m$：点数和边数。
• $U,V$：$\forall 0\le i\lt m$，都有 $(U[i],V[i])\in E$。
• 返回一个非负整数，表示完美数列不等对数量的最大值。

输入格式

Sample Grader 输入格式如下：

第一行，两个正整数 $n,m$。

接下来 $m$ 行，第 $i$ 行两个非负整数 $U[i-1],V[i-1]$。

输出格式

输出一行一个非负整数，表示答案。

5 5
0 1
0 2 
1 2
1 3
2 4

7

提示

样例交互

样例交互 $1$

$n = 5, m = 5, U = [0, 0, 1, 1, 2],V=[1, 2, 2, 3, 4]$。

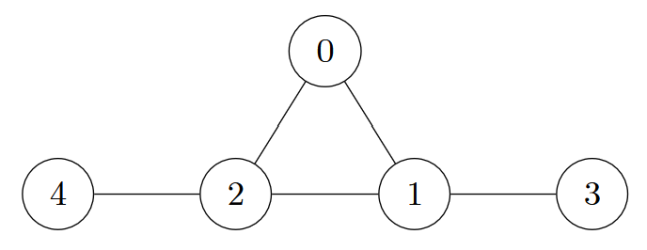
$a=[2,1,1,3,1]$ 不是完美的。取路径 $u_0=0,u_1=1,u_2=3$，则 $a_{u_0}=2,a_{u_1}=1,a_{u_2}=3$，不满足条件。

$[1,1,1,1,1]$ 是完美的，不等对数量为 $0$。

$[2,2,2,3,0]$ 是完美的，不等对数量为 $7$。

可以证明完美数列中，不等对数量最大值为 $7$。故返回 $7$。

数据范围

• $2\le n\le 10^6$；
• $1\le m\le 2\times 10^6$；
• $U[i]\neq V[i]$；
• $0\le U[i],V[i]\lt n$。

子任务

子任务编号	$n\le$	$m\le$	特殊性质	得分
$1$	$500$		$\text{AB}$	$1$
$2$	$5\times 10^3$			$4$
$3$	$10^6$			$5$
$4$	$500$		$\text{B}$	$3$
$5$	$5\times 10^3$			$5$
$6$	$10^6$			$28$
$7$	$500$	$10^3$	/	$6$
$8$	$5\times 10^3$	$10^4$		$10$
$9$	$10^6$	$2\times 10^6$		$38$

• 特殊性质 $\text{A}$：每个点的度数都不大于 $4$。
• 特殊性质 $\text{B}$：$m=n-1$。