本题没有可用的提交语言。

题目背景

搬运自 2012 年清华大学信息学邀请赛。

题目描述

有一个正方形的地区，该地区特点鲜明：如果把它等分为 $N\times N$ 个小正方形格子的话，在每个格子内的任意地点的地表高度是相同的，并且是一个 $0$ 到 $M$ 之间的整数。正方形地区的外部被无限高的边界包围。

该地区可能会有积水。经过多年的观察，人们发现了几个关于积水的重要规律：

1. 每个格子要么完全没有积水，要么它内部的任意地点的水面高度都是相同的。并且水面高度一定大于地表高度。
2. 每个格子的水面高度在 $0\sim m$之间，并且一定是整数。
3. 对于相邻（必须为边相邻）的两个格子，一定不会出现水自动从一个格子流向另一个格子的情况。也就是说，一定不能出现这两个格子都有水且水面高度不同，或者有水格子的水面比无水格子的地表要高的情况。

例如，下面图中每个格子里有两个数 $a/b$，说明该格子的地表高度是 $a$，水面高度是 $b$（均为海拔高度），而没有水的格子中 $b$ 以 - 表示。则左边的情况是符合规律的，而右边的情况并不符合以上规律，因为水可以由 $2/4$ 的格子流向 $3/-$ 的格子。

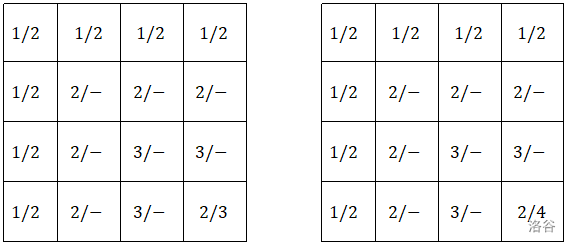
该地区水文站的工作人员小 A 想知道，该地区中有多少种不同的水位情况符合规律。你能回答他的这个问题吗？

输入格式

输入文件的第一行包含两个正整数 $N$ 和 $M$。

随后的 $N$ 行，每行包含 $N$ 个非负整数。其中第 $i+1$ 行的第 $j$ 个数表示该地区第 $i$ 行第 $j$ 列格子的地表高度。

输出格式

输出文件只包含一个整数，即该地区符合规律的水位情况种数。

4 3
1 1 1 1
1 2 2 2
1 2 3 3
1 2 3 2

6

提示

【对样例的说明】

符合规律的水位情况有以下六种：

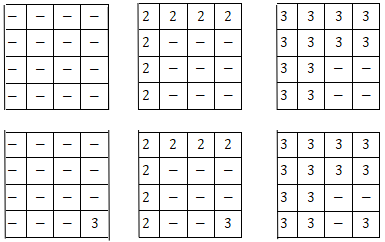
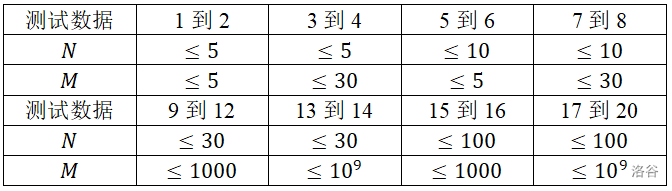
【数据规模与约定】