本题没有可用的提交语言。

题目背景

搬运自 2014 年清华大学信息学邀请赛。

题目描述

Printed Circuit Board（简称PCB），印刷电路板，它可以固定各种电子元器件，然后将它们连接起来，使得整个系统能够实现我们所需要的功能。因此，“焊板子”是一个很多工科学生（尤其是电子、自动化系的同学）都需要掌握的技能。

现代电路板多用印刷技术制成。印刷线路板的最大特点是装配的元件紧凑、美观，并且适合于工厂的大规模生产。当然也适合各种电子小制作。这种线路板的基板是矩形的，用环氧板或纸质板制成。在基板上面用热压工艺贴上一层很薄的铜箔。用印刷法把电路印在铜箔上，再用腐蚀法把不需要的铜箔去掉，留下的铜箔便构成电路，最后钻上小孔，涂上助焊保护剂，电路板便制成了。

由于技术的限制，电路板上铜线的宽度是确定的，并且铜线必须平行于电路板的边界（也就是说铜线必须平行于坐标轴）。

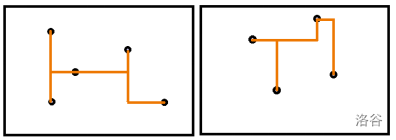
例如以上两幅图都是可行的电路板。

现在 R 同学需要制作很多很多电路板，每个电路板上有若干个电子元件。他需要合理布置电路使得铜箔将所有电子元件都连通，并且消耗的铜最少。

输入格式

第一行输入两个正整数 $T,n$，表示R同学需要制作的电路板数量和每块电路板上的电子元件数。

由于输入数据规模庞大，因此采用输入种子后随机生成的方式。

第二行输入 $6$ 个正整数 $a,c,Mx,My,seedx,seedy$，以及一个字符 $datatype$，并用以下方式生成序列 $X_i,Y_i$：

$$X_0=seedx, X_i=((aX_{i-1}+c) \div 2^{16})\bmod 2^{16} $$$$Y_0=seedy, Y_i=((aY_{i-1}+c) \div 2^{16})\bmod 2^{16} $$

若 $datatype$ 为 B，则：

$$(X_{in}\bmod Mx+Mx,Y_{in}\bmod My+My)$$ $$(X_{in+1}\bmod Mx+Mx,Y_{in+1}\bmod My+My)$$ $$(X_{in+2}\bmod Mx+Mx,Y_{in+2}\bmod My+My)$$ $$(X_{in+3}\bmod Mx+Mx,Y_{in+}\bmod My+My)$$ $$\dots$$ $$(X_{in+n-1}\bmod Mx_+Mx,Y_{in+n-1}\bmod My+My)$$

为第 $i (0 \le i \lt T)$ 组数据中的 $n$ 个电子元件的坐标。

若 $datatype$ 为 B，则：

$$(X_{in}\bmod Mx+Mx,Y_{in}\bmod My+My)$$ $$(X_{in+1}\bmod Mx+Mx,Y_{in+1}\bmod My+My)$$ $$(X_{in+2}\bmod Mx+Mx,Y_{in+2}\bmod My+My)$$ $$(X_{in+3}\bmod Mx,Y_{in+3}\bmod My)$$ $$\dots$$ $$(X_{in+n-1}\bmod Mx,Y_{in+n-1}\bmod My)$$

为第 $i (0 \le i \lt T)$ 组数据中的 $n$ 个电子元件的坐标。（即前三个点的横纵坐标分别加上 $Mx$ 和 $My$）。

输出格式

每组数据输出一行，仅包含一个数，表示最短的铜线长度。

3 3
903527 47001 10 10 675 293 A

11
5
9

8 5
903527 47001 5 5 190 338 A

9
8
7
7
8
7
8
4

5 7
903527 47001 1000 1000 190 338 B

3364
3305
4076
3714
2969

提示

【样例 #1 解释】

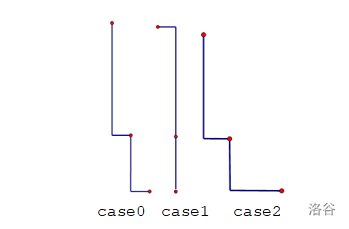
case0:(5,3) (6,0) (4,9) 
case1:(2,1) (1,4) (2,0) 
case2:(1,3) (0,7) (3,1)

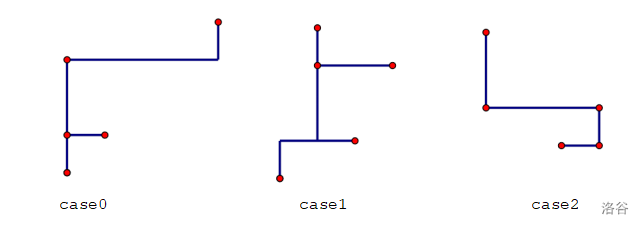
【样例 #2 解释】

case0: (0,3) (0,0) (1,1) (4,4) (0,1)
case1: (3,1) (2,3) (2,4) (4,3) (1,0)
case2: (3,2) (2,1) (0,2) (0,4) (3,1)

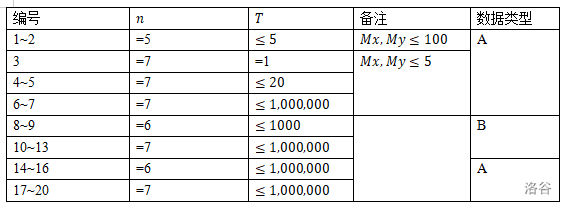
【数据范围】

对于 $100\%$ 的数据，$n \le 7,T \le 10^6, a,c < 2^{31},Mx,My \le 2^{16}$。

本题共 $20$ 组数据，每组 $5$ 分。

【小贴士】

为了方便大家编写程序，在这里提供一个上述的数据生成的代码，仅供大家参考（不必以此为模板）。

C/C++：

int X[7000010],Y[7000010];
int n,T,a,c,Mx,My;
long long seedx,seedy;
char datatype[4];
//生成数据，并将其对Mx，My取模后的值保存在X,Y这两个数组中
void createList() {
int AD = (1 << 16) - 1;
  int i;
  for (i = 0;i < n*T;i++) {
    X[i] = seedx % Mx;
    Y[i] = seedy % My;
if (i % n < 3 && datatype[0] == 'B')
X[i] += Mx,Y[i] += My;
    seedx = (((a * seedx + c) >> 16) & AD);
    seedy = (((a * seedy + c) >> 16) & AD);
  }
}

int main() {
  scanf("%d%d%d%d%d%d%d%d%s",
&T, &n, &a, &c, &Mx, &My, &seedx, &seedy, datatype);
  createList();
//你的计算代码
  return 0;
}

Pascal：

var 
  ax,ay:array[0..7000000] of longint;
  n,T,a,c,Mx,My:longint;
  seedx,seedy:int64;
  datatype:char;
  i,j:longint;
//生成数据，并将其对Mx，My取模后的值保存在ax,ay这两个数组中
procedure createList;
var AD,i:longint;
begin
  AD := (1 shl 16) - 1;
  for i:=0 to n * T - 1 do
  begin
    ax[i] := seedx mod Mx;
    ay[i] := seedy mod My;
    if ((i mod n < 3) and (datatype = 'B')) then
    begin
      ax[i] := ax[i] + Mx;
      ay[i] := ay[i] + My;
    end;
    seedx := (((a * seedx + c) shr 16) and AD);
    seedy := (((a * seedy + c) shr 16) and AD);
  end;
end;
begin
  read(T,n,a,c,Mx,My,seedx,seedy);
  read(datatype);
  while (datatype = ' ') do read(datatype);
  createList;
  //你的计算代码
end.