本题没有可用的提交语言。

题目背景

搬运自 2014 年清华大学信息学邀请赛。

题目描述

$\bf{B}$ 君得到了一个神奇的超立方体，具体来说这是一个 $m$ 维的超立方体，一共有 $n=2^m$ 个顶点，我们将这些点从 $0$ 到 $n-1$ 标号。

对于点 $i$，我们可以把 $i$ 转换成 $m$ 位二进制表示，如果不足 $m$ 位则高位补 $0$。这样得到的一个 $m$ 维坐标就是这个点的坐标。

如果两个点的欧几里得距离为 $1$（也就是说，在原先的超立方体中有一条边连接它们），那么它们是相邻的。

点 $i$ 有 $p_i$ 个信息，每过一个周期，每个点都会向相邻节点发送这些信息，且自己不保留这些信息。具体来说，点 $i$ 的信息总和变为它相邻的 $m$ 个点的信息和。

现在 $\bf{B}$ 君已知 $n$ 个点的初始信息 $p_i$，他想预言 $t$ 个周期之后所有点的信息分别是多少。

$\bf{B}$ 君对此一筹莫展，于是找到了他的好朋友 $\bf{R}$ 君。

$\bf{R}$ 君：“$n$ 和 $t$ 有多大？”

$\bf{B}$ 君：“$n$ 大约是 $2^{20}$，$t$ 大约是 $10^{18}$。”

$\bf{R}$ 君：“那这个结果太大了，即便算出来，也根本存不下。”

$\bf{B}$ 君：“那么就将最终结果模一个数吧。”

$\bf{R}$ 君：“那我再来想想看。”

输入格式

第一行三个整数 $n,t$ 和 $K$，其中 $K$ 为 $32$ 为符号整数。

以下 $n$ 行，每行一个整数 $p_i(p_i<K)$，含义如题目描述。

输出格式

一共 $n$ 行，每行一个整数 $q_i$，表示 $t$ 个周期后 $i$ 节点信息总和除以 $K$ 的余数。

4 2 10007
4
1
2
3

14
6
6
14

提示

【对样例的说明】

【数据规模与约定】

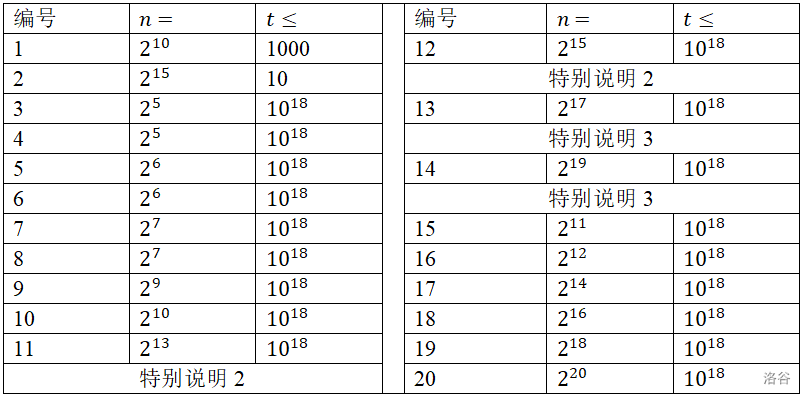
• 特别说明 $1$：所有编号为奇数的测试点，$K$ 为合数；所有编号为偶数的测试点，$K$ 为质数。
• 特别说明 $2$：最开始时，有超过 $20$ 个点上没有任何信息。
• 特别说明 $3$：最开始时，仅有 $5$ 个点上存有信息。